Chapter 6 Using the EIF to construct an estimator: the case of the natural direct effect

6.1 Natural direct effect

Recall:

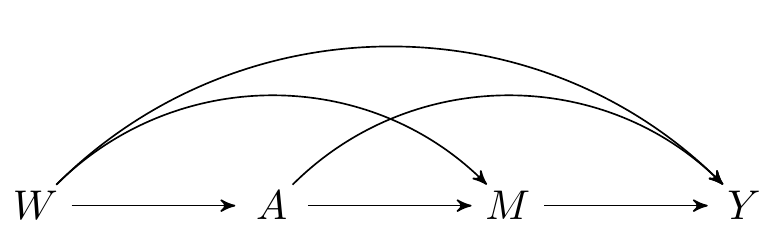
Directed acyclic graph under *no intermediate confounders* of the mediator-outcome relation affected by treatment

FIGURE 2.1: Directed acyclic graph under no intermediate confounders of the mediator-outcome relation affected by treatment

  • Assuming a binary \(A\), we define the natural direct effect as: \[NDE = E(Y_{1,M_{0}} - Y_{0,M_{0}}),\]

  • and the natural indirect effect as: \[NIE = E(Y_{1,M_{1}} - Y_{1,M_{0}}).\]

  • The observed data is \(O=(W, A, M, Y)\)

This SCM is represented in the above DAG and the following causal models: \[\begin{align*} W & = f_W(U_W)\\ A & = f_A(W, U_A)\\ M & = f_M(W, A, U_M)\\ Y & = f_Y(W, A, M, U_Y), \end{align*}\] where \((U_W, U_A,U_M, U_Y)\) are exogenous random errors.

We assume - \(A\) is a single binary randomized treatment (and thus \(A = f_A(U_A)\)) - \(M\) is a single binary mediator - There are no restrictions on the distribution of \(W\) or \(Y\)

Recall that we need to assume the following to identify the above caual effects from our observed data:

  • \(A \indep Y_{a,m} \mid W\)
  • \(M \indep Y_{a,m} \mid W, A\)
  • \(A \indep M_a \mid W\)
  • \(M_0 \indep Y_{1,m} \mid W\)
  • and positivity assumptions

Then, the NDE is identified as \[\begin{equation*} \psi(\P) = \E[\E\{\E(Y \mid A=1, M, W) - \E(Y \mid A=0, M, W)\mid A=0,W\}] \end{equation*}\]

6.1.1 The efficient influence function for the NDE

  • For illustration, we will first present how to construct an estimator of the NDE that uses the EIF ``by hand’’
  • For other parameters, we will teach you how to use our packages medoutcon and medshift

First, we need to introduce some notation to describe the EIF for the NDE

  • Let \(Q(M, W)\) denote \(\E(Y\mid A=1, M, W) - \E(Y\mid A=0, M, W)\)

  • We can now introduce the EIF: \[\begin{align*} D(O) &= \color{RoyalBlue}{\bigg\{ \frac{I(A=1)}{\P(A=1\mid W)}\frac{\P(M\mid A=0,W)}{\P(M\mid A=1,W)} - \frac{I(A=0)}{\P(A=0\mid W)}\bigg\}} \times \color{Goldenrod}{[Y-\E(Y\mid A,M,W)]} \\ &+ \color{RoyalBlue}{\frac{I(A=0)}{\P(A=0\mid W)}}\color{Goldenrod}{\big\{Q(M,W) - \E[Q(M,W) | W,A=0] \big\}}\\ &+ \color{Goldenrod}{\E[Q(M,W) | W,A=0] - \psi(\P)} \end{align*}\]

  • In this EIF, you can recognize elements from the g-computation estimator and the weighted estimator:

    • \(Q(M, W)\) shows up in the g-computation estimator
    • The weights in blue in the first part of the EIF are used in the weighted estimator

  • Estimating \(\P(M\mid A, W)\) is a really hard problem when \(M\) is high-dimensional. But, since we have the ratio of these conditional densitities, we can reparamterize using Bayes rule to get something that is easier to compute:

\[\begin{equation*} \frac{\P(M\mid A=0,W)}{\P(M\mid A=1,W)} = \frac{\P(A = 0 \mid M, W) \P(A=1 \mid W)}{\P(A = 1 \mid M, W)\P(A=0 \mid W)}. \end{equation*}\]

Thus we can change the expression of the EIF a bit as follows. First, some more notation that will be useful later:

  • Let \(g(a\mid w)\) denote \(\P(A=a\mid W=w)\)
  • Let \(e(a\mid m, w)\) denote \(\P(A=a\mid M=m, W=w)\)
  • Let \(b(a, m, w)\) denote \(\E(Y\mid A=a, M=m, W=w)\)
  • The EIF is

\[\begin{align*} D(O) &= \color{RoyalBlue}{\bigg\{ \frac{I(A=1)}{g(0\mid W)}\frac{e(0\mid M,W)}{e(1\mid M,W)} - \frac{I(A=0)}{g(0\mid W)}\bigg\}} \times \color{Goldenrod}{[Y-b(A,M,W)]} \\ &+ \color{RoyalBlue}{\frac{I(A=0)}{g(0\mid W)}}\color{Goldenrod}{\big\{Q(M,W) - \E[Q(M,W) | W,A=0] \big\}}\\ &+ \color{Goldenrod}{\E[Q(M,W) | W,A=0] - \psi(\P)} \end{align*}\]

6.1.2 How to compute the one-step estimator (akin to Augmented IPW)

First we will generate some data:

mean_y <- function(m, a, w) abs(w) + a * m
mean_m <- function(a, w)plogis(w^2 - a)
pscore <- function(w) plogis(1 - abs(w))

w_big <- runif(1e6, -1, 1)
trueval <- mean((mean_y(1, 1, w_big) - mean_y(1, 0, w_big)) * mean_m(0, w_big)
                + (mean_y(0, 1, w_big) - mean_y(0, 0, w_big)) *
                  (1 - mean_m(0, w_big)))

n <- 1000
w <- runif(n, -1, 1)
a <- rbinom(n, 1, pscore(w))
m <- rbinom(n, 1, mean_m(a, w))
y <- rnorm(n, mean_y(m, a, w))

Recall that the one-step estimator is defined as the bias-corrected g-computation estimator: \[\begin{equation*} \psi(\hat \P) + \frac{1}{n}\sum_{i=1}^n D(O;\hat \P_i) \end{equation*}\]

Can be computed in the following steps:

  1. Fit models for \(g(a\mid w)\), \(e(a\mid m, w)\), and \(b(a, m, w)\)
    • In this example we will use Generalized Additive Models for tractability
    • In applied settings we recommend using an ensemble of data-adaptive regression algorithms, such as the Super Learner (van der Laan, Polley, and Hubbard 2007)
library(mgcv)
## fit model for E(Y | A, W)
b_fit <- gam(y ~ m:a + s(w, by = a))
## fit model for P(A = 1 | M, W)
e_fit <- gam(a ~ m + w + s(w, by = m), family = binomial)
## fit model for P(A = 1 | W)
g_fit <- gam(a ~ w, family = binomial)
  1. Compute predictions \(g(1\mid w)\), \(g(0\mid w)\), \(e(1\mid m, w)\), \(e(0\mid m, w)\),\(b(1, m, w)\), \(b(0, m, w)\), and \(b(a, m, w)\)
## Compute P(A = 1 | W)
g1_pred <- predict(g_fit, type = 'response')
## Compute P(A = 0 | W)
g0_pred <- 1 - g1_pred
## Compute P(A = 1 | M, W)
e1_pred <- predict(e_fit, type = 'response')
## Compute P(A = 0 | M, W)
e0_pred <- 1 - e1_pred
## Compute E(Y | A = 1, M, W)
b1_pred <- predict(b_fit, newdata = data.frame(a = 1, m, w))
## Compute E(Y | A = 0, M, W)
b0_pred <- predict(b_fit, newdata = data.frame(a = 0, m, w))
## Compute E(Y | A, M, W)
b_pred  <- predict(b_fit)
  1. Compute \(Q(M, W)\), fit a model for \(\E[Q(M,W) | W,A]\), and predict at \(A=0\)
## Compute Q(M, W)
pseudo <- b1_pred - b0_pred
## Fit model for E[Q(M, W) | A, W]
q_fit <- gam(pseudo ~ a + w + s(w, by = a))
## Compute E[Q(M, W) | A = 0, W]
q_pred <- predict(q_fit, newdata = data.frame(a = 0, w = w))
  1. Estimate the weights \[\begin{equation*} \color{RoyalBlue}{\bigg\{ \frac{I(A=1)}{g(0\mid W)}\frac{e(0\mid M,W)}{e(1\mid M,W)} - \frac{I(A=0)}{g(0\mid W)}\bigg\}} \end{equation*}\] using the above predictions:
ip_weights <- a / g0_pred * e0_pred / e1_pred - (1 - a) / g0_pred
  1. Compute the uncentered EIF:
eif <- ip_weights * (y - b_pred) + (1 - a) / g0_pred * (pseudo - q_pred) +
  q_pred
  1. The one step estimator is the mean of the uncentered EIF

## One-step estimator
mean(eif)
#> [1] 0.55085

6.1.3 Performance of the one-step estimator in a small simulation study

First, we create a wrapper around the estimator

one_step <- function(y, m, a, w) {
  b_fit <- gam(y ~ m:a + s(w, by = a))
  e_fit <- gam(a ~ m + w + s(w, by = m), family = binomial)
  g_fit <- gam(a ~ w, family = binomial)
  g1_pred <- predict(g_fit, type = 'response')
  g0_pred <- 1 - g1_pred
  e1_pred <- predict(e_fit, type = 'response')
  e0_pred <- 1 - e1_pred
  b1_pred <- predict(b_fit, newdata = data.frame(a = 1, m, w),
                 type = 'response')
  b0_pred <- predict(b_fit, newdata = data.frame(a = 0, m, w),
                     type = 'response')
  b_pred  <- predict(b_fit, type = 'response')
  pseudo <- b1_pred - b0_pred
  q_fit <- gam(pseudo ~ a + w + s(w, by = a))
  q_pred <- predict(q_fit, newdata = data.frame(a = 0, w = w))
  ip_weights <- a / g0_pred * e0_pred / e1_pred - (1 - a) / g0_pred
  eif <- ip_weights * (y - b_pred) + (1 - a) / g0_pred *
    (pseudo - q_pred) + q_pred
  return(mean(eif))
}

Let us first examine the bias

  • The true value is:
w_big <- runif(1e6, -1, 1)
trueval <- mean((mean_y(1, 1, w_big) - mean_y(1, 0, w_big)) * mean_m(0, w_big) +
  (mean_y(0, 1, w_big) - mean_y(0, 0, w_big)) * (1 - mean_m(0, w_big)))
print(trueval)
#> [1] 0.58061
  • Bias simulation
estimate <- lapply(seq_len(1000), function(iter) {
  n <- 1000
  w <- runif(n, -1, 1)
  a <- rbinom(n, 1, pscore(w))
  m <- rbinom(n, 1, mean_m(a, w))
  y <- rnorm(n, mean_y(m, a, w))
  estimate <- one_step(y, m, a, w)
  return(estimate)
})
estimate <- do.call(c, estimate)

hist(estimate)
abline(v = trueval, col = "red", lwd = 4)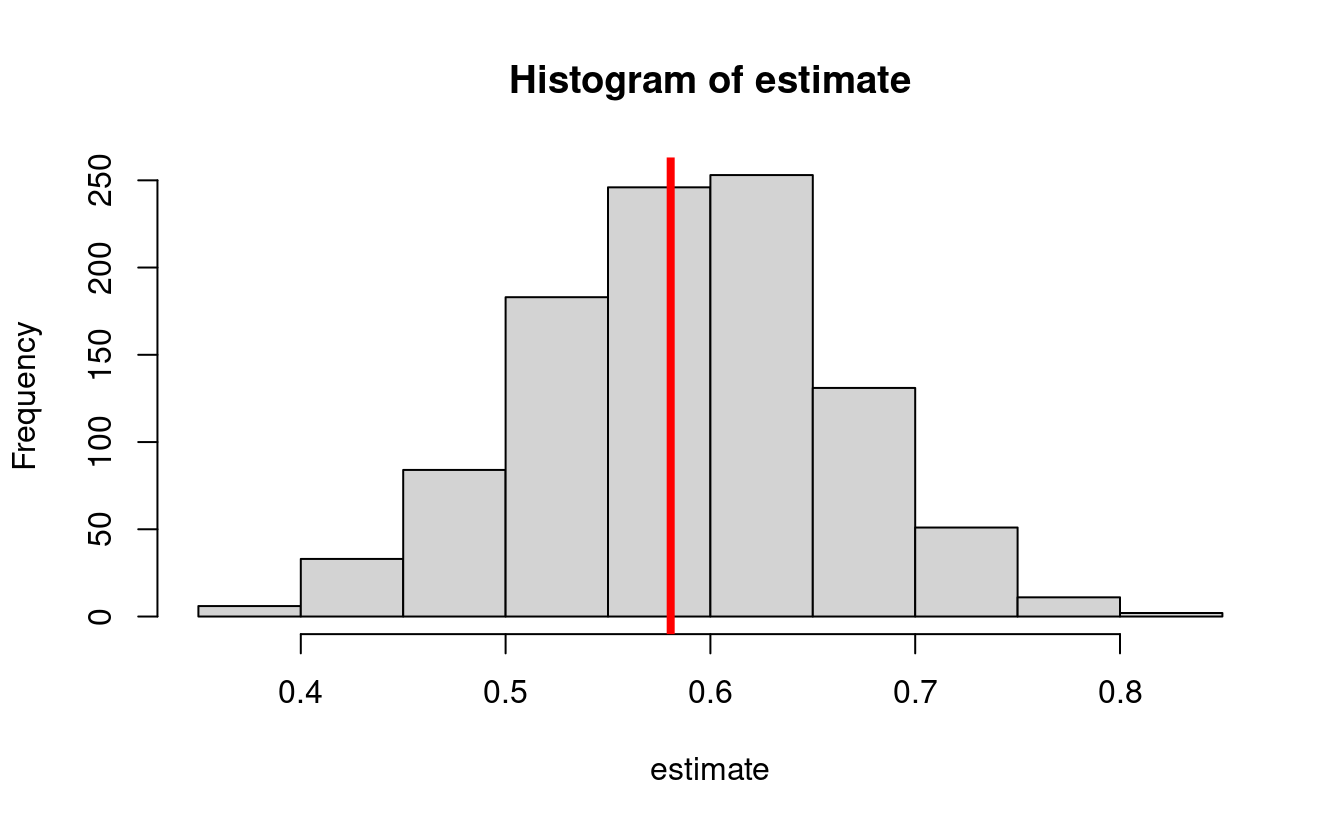

  • And now the confidence intervals:
cis <- cbind(
  estimate - qnorm(0.975) * sd(estimate),
  estimate + qnorm(0.975) * sd(estimate)
)

ord <- order(rowSums(cis))
lower <- cis[ord, 1]
upper <- cis[ord, 2]
curve(trueval + 0 * x,
  ylim = c(0, 1), xlim = c(0, 1001), lwd = 2, lty = 3, xaxt = "n",
  xlab = "", ylab = "Confidence interval", cex.axis = 1.2, cex.lab = 1.2
)
for (i in 1:1000) {
  clr <- rgb(0.5, 0, 0.75, 0.5)
  if (upper[i] < trueval || lower[i] > trueval) clr <- rgb(1, 0, 0, 1)
  points(rep(i, 2), c(lower[i], upper[i]), type = "l", lty = 1, col = clr)
}
text(450, 0.10, "n=1000 repetitions = 1000 ", cex = 1.2)
text(450, 0.01, paste0(
  "Coverage probability = ",
  mean(lower < trueval & trueval < upper), "%"
), cex = 1.2)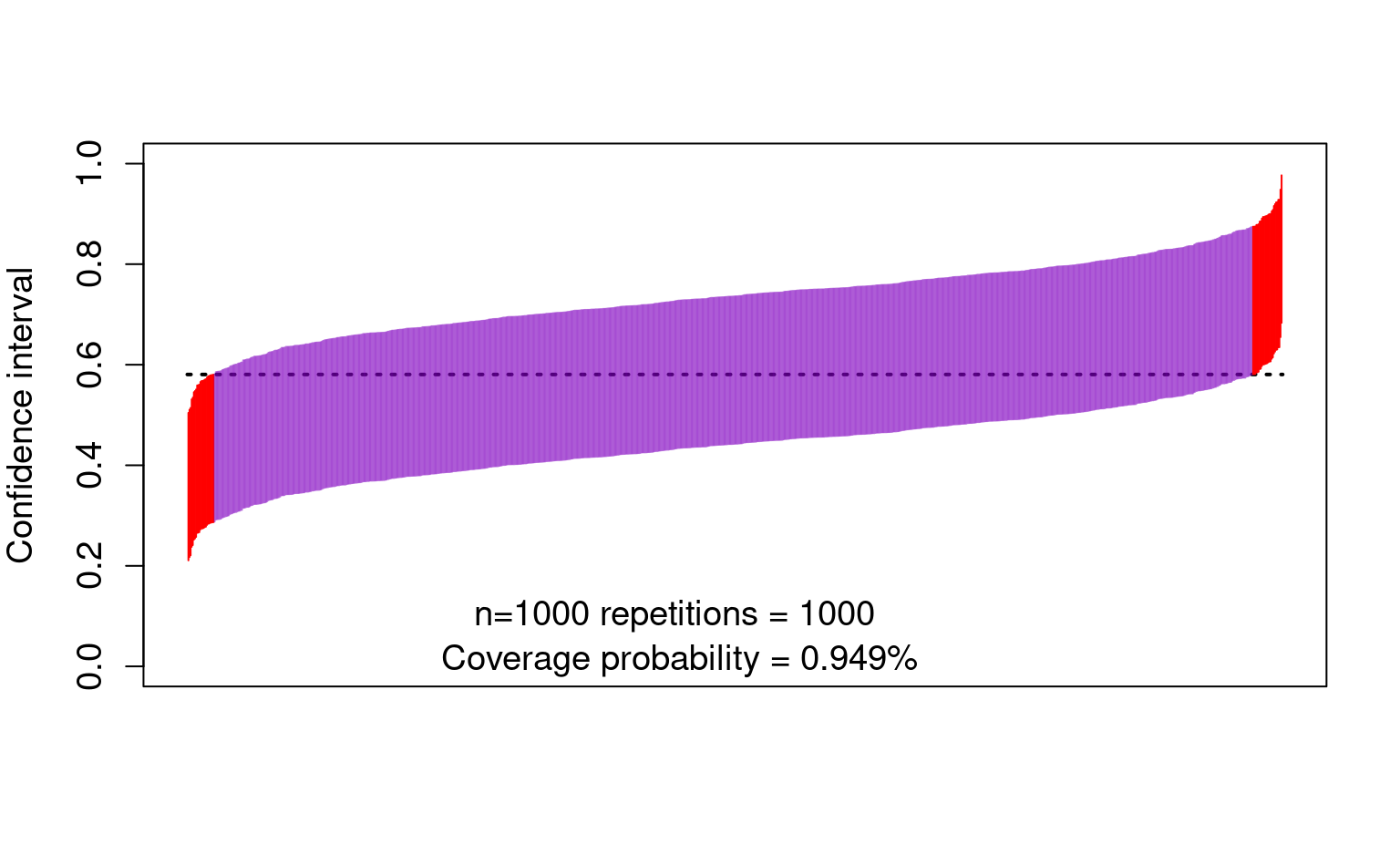

6.1.4 A note about targeted minimum loss-based estimation (TMLE)

  • The above estimator is great because it allows us to use data-adaptive regression to avoid bias, while allowing the computation of correct standard errors
  • This estimator has one problem:
    • It can yield answers outside of the bounds of the parameter space
    • E.g., if \(Y\) is binary, it could yield direct and indirect effects outside of \([-1,1]\)
    • To solve this, you can compute a TMLE instead (implemented in the R packages, coming up)

6.1.5 A note about cross-fitting

  • When using data-adaptive regression estimators, it is recommended to use cross-fitted estimators
  • Cross-fitting is similar to cross-validation:
    • Randomly split the sample into K (e.g., K=10) subsets of equal size
    • For each of the 9/10ths of the sample, fit the regression models
    • Use the out-of-sample fit to predict in the remaining 1/10th of the sample
  • Cross-fitting further reduces the bias of the estimators
  • Cross-fitting aids in guaranteeing the correctness of the standard errors and confidence intervals
  • Cross-fitting is implemented by default in the R packages that you will see next